Управление рисками с помощью опционов
Скачать PDF | Загрузок: 1
Статья в журнале
Российское предпринимательство *
№ 11 (71), Ноябрь 2005
* Этот журнал не выпускается в Первом экономическом издательстве
Цитировать:
Селюков В.К. Управление рисками с помощью опционов // Российское предпринимательство. – 2005. – Том 6. – № 11. – С. 58-61.
Аннотация:
Несмотря на то, что модель Блэка-Шоулза создана для европейского опциона , разрабатывать специальную модель для оценки стоимости европейского опциона не требуется. Такая модель может быть легко получена на основе паритета цен европейских опционов и , вытекающего из теоремы «пут-колл эквивалентности». Существо этой теоремы может быть продемонстрировано на примере выполнения некоторым лицом серии финансовых операций.
Ключевые слова: акции, реальный опцион
Продолжение. Начало в №№ 11, 12/2003, 4, 5, 6, 7, 9, 10, 12, /2004, 1, 4, 5, 6, 7, 8, 9 /2005
Паритет цен европейских Call и Put опционов
Несмотря на то, что модель Блэка-Шоулза создана для европейского опциона , разрабатывать специальную модель для оценки стоимости европейского опциона не требуется. Такая модель может быть легко получена на основе паритета цен европейских опционов и , вытекающего из теоремы «пут-колл эквивалентности».
Существо этой теоремы может быть продемонстрировано на примере выполнения некоторым лицом серии финансовых операций.
В какой-то исходный момент времени выполняются следующие операции:
Совокупный денежный поток при совершении этих сделок будет равен значению![]()
По истечении времени (в момент времени исполнения опционов), независимо от цены базового актива, возвращается кредит в размере . Другие действия будут зависеть от складывающейся на рынке цены базового актива . Возможны три ситуации:
1) . ![]() В этом случае опцион Call «в деньгах» и будет исполнен. Продавец опциона поставляет базовый актив по цене . Вырученная продавцом сумма целиком идёт на погашение кредита. Опцион оказался «вне денег» и поэтому исполняться не будет. В результате чистый поток денежных средств будет равен нулю;
В этом случае опцион Call «в деньгах» и будет исполнен. Продавец опциона поставляет базовый актив по цене . Вырученная продавцом сумма целиком идёт на погашение кредита. Опцион оказался «вне денег» и поэтому исполняться не будет. В результате чистый поток денежных средств будет равен нулю;
2) . ![]() В этой ситуации опцион «вне денег» и исполняться не будет. Опцион «в деньгах» и исполняется. Владелец опциона продаёт базовый актив по цене . Вырученная им сумма целиком идёт на погашение кредита. Чистый поток денежных средств опять равен нулю.
В этой ситуации опцион «вне денег» и исполняться не будет. Опцион «в деньгах» и исполняется. Владелец опциона продаёт базовый актив по цене . Вырученная им сумма целиком идёт на погашение кредита. Чистый поток денежных средств опять равен нулю.
3) . ![]() В этом маловероятном случае оба опциона «на деньгах» и исполняться не будут. Базовый актив продаётся по рыночной цене . Полученная сумма целиком идёт на погашение кредита. И в этом случае чистый денежный поток равен нулю.
В этом маловероятном случае оба опциона «на деньгах» и исполняться не будут. Базовый актив продаётся по рыночной цене . Полученная сумма целиком идёт на погашение кредита. И в этом случае чистый денежный поток равен нулю.
Таким образом, во всех случаях проведённая совокупность финансовых операций приводит к нулевому чистому денежному потоку. То есть, итоговая стоимость рассматриваемого портфеля для любого значения t равна нулю. На основании этого можно сделать вывод, что и начальная стоимость портфеля также равна нулю.![]()
Если бы это равенство не выполнялось, то появлялась бы возможность совершения арбитражных сделок и получения безрисковой прибыли.
Полученное выражение позволяет производить оценку стоимости опциона по известной оценке стоимости опциона:![]()
Коэффициенты чувствительности опционов
Как отмечалось ранее, стоимость опционного контракта зависит от целого ряда факторов. где дельта, тета, ро и вега – коэффициенты чувствительности стоимости опциона.
где дельта, тета, ро и вега – коэффициенты чувствительности стоимости опциона.
В процессе управления рисками возникает необходимость в оценке указанных и ряда других коэффициентов чувствительности.
Коэффициент дельта
Коэффициент дельта () – это параметр, характеризующий чувствительность стоимости опциона (премии) к изменению цены базового актива.

Более детальное рассмотрение коэффициента дельта удобно осуществить на конкретном примере (рис. 5). На этом рисунке представлена зависимость стоимости -опциона на сто акций одного из эмитентов от цены базового актива (кривая линия). На рис. 5 также отражена внутренняя стоимость опциона в виде прямолинейных отрезков.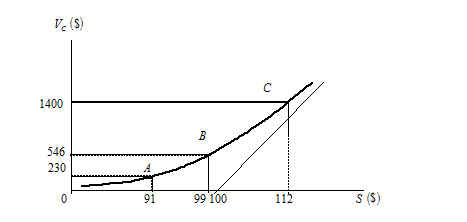 Рис. 5. График зависимости стоимости опциона от цены базового актива
Рис. 5. График зависимости стоимости опциона от цены базового актива
На рис. 5 обозначены три характерные точки: , , . В точке (91, 230) опцион вне денег. Если цена акций увеличится или уменьшится на небольшую величину, например, на $0,1, то стоимость опционного контракта увеличится или уменьшится на $3. Хотя объём контракта 100 акций, в точке он ведёт себя так, будто исполнение может произойти только на 30 акций. Стоимость опциона изменяется так, как изменялась бы стоимость портфеля, состоящего только из части лота акций, на который был выписан контракт. Эта часть (30/100 = 0,3) и представляет собой дельту в точке .
В точке (99, 546) опцион на деньгах. В этой точке стоимость опциона изменяется так, как изменялась бы стоимость портфеля, состоящего из 50 акций. Здесь дельта равна 0,5 (50/100).
В точке (112, 1400) опцион в деньгах. В этой точке стоимость опциона изменяется так, как изменялась бы стоимость портфеля, состоящего из 80 акций. То есть, дельта равна 0,8 (80/100).
Выше точки опцион глубоко в деньгах. По мере роста цены акций стоимость опциона также продолжает расти. Дельта приближается к единице. В этом случае изменение в стоимости опциона в точности повторяет изменение в стоимости 100 акций.
Ниже точки (опцион глубоко вне денег) стоимость опциона и дельта стремятся к нулю.
Таким образом, для длинного -опциона коэффициент чувствительности дельта изменяется от 0 до 1.
Продолжение следует
Страница обновлена: 22.01.2024 в 18:25:52
