Об одном способе расчета инвестиций для импортозамещения продовольственных продуктов

Указ Президента России от 6 августа 2014 года и постановление Правительства России о запрете ввоза продовольственных товаров из некоторых стран Запада открыли, по сути, новую страницу развития отечественной пищевой и перерабатывающей промышленности. Становятся все более актуальными проблемы продовольственной безопасности России. Одной из таких проблем является проблема инвестиционного обеспечения импортозамещения продуктов питания. Прежде чем начать обсуждение данной проблемы, дадим краткую характеристику современного состояния пищевой и перерабатывающей промышленности. По данным Росстата, в которых отрасль названа как «производство пищевых продуктов, включая напитки, и табака» [1], пищевая и перерабатывающая промышленность занимает достаточно высокое место в структуре отгруженной продукции обрабатывающих производств России, на ее долю приходилось в 2012 г. 15,9% или 4001 млрд руб. в ценах этого года. В структуре валовой добавленной стоимости за 2013 г. в текущих ценах 2008 г. добавленная стоимость, созданная в пищевой и перерабатывающей промышленности, составила около 2,5%.

В 2012 г. пищевая и перерабатывающая промышленность состояла из более 43000 предприятий (около 17% от общего количества в обрабатывающих производствах), на которых было занято около 1,3 млн человек (16,7% соответственно). На ее долю приходилось около 16% основных фондов всех обрабатывающих производств [1].

Несмотря на то, что в 2011 г. отрасль снизила темпы производства по сравнению с 2010 г., в 2012 г. она снова возросла на 5,1% [1].

Можно с уверенностью говорить о том, что в 2014 г. в отрасли продолжали устаревать высоко изношенные основные фонды, наблюдались недостаточность инвестиций, слабая инновационная деятельность. В конечном итоге именно состояние производственного аппарата отрасли предопределяет возникновение серьезнейших проблем в инвестиционном обеспечении продовольственной безопасности России. Эти проблемы особенно заметны на фоне современных условий функционирования отраслей пищевой и перерабатывающей промышленности в индустриально развитых странах, для которых характерен более высокий технический уровень производства, базирующийся на современных достижениях научно-технического прогресса и эффективные меры защиты собственных продовольственных рынков.

Сколько замещать показывают данные по импорту продовольственных товаров. В 2012 году на продовольственном рынке страны за счет импорта формировалось почти 23% ресурсов мяса и мясопродуктов, почти 17% рыбы и рыбопродуктов и 20% молока и молокопродуктов [1]. Отметим, что в последнее время, в связи с известными событиями, импорт отдельных видов продовольственных товаров снизился. Так, в январе-июле 2014 г. к соответствующему периоду 2013 г. импорт мяса, свежего и мороженного, составил около 80%, молока и сливок сгущенных – 75%, сыров и творога – 87%, растительных масел – 36% [2].

Из-за действия санкций, вероятно, он будет снижаться и в 2015 г., что должно вызвать нарастание остроты проблемы компенсации снижения импорта за счет собственного производства. Как известно, в сентябре 2014 года Правительство РФ утвердило так называемую «дорожную карту» по импортозамещению продовольствия [3]. По этой карте должно произойти снижение зависимости внутреннего рынка от импортных поставок мяса с 21,6 до 7,7%, молока и молочной продукции – с 23,6 до 16,6%, овощей – с 14,6 до 10,1% к 2020 году. В «дорожной карте» предусматривается комплекс мер, таких как субсидирование процентных ставок по кредитам для сельхозпроизводителей и цен на приобретение ими сельхозтехники; инвестиции в проекты по повышению плодородия сельскохозяйственных почв и племенного дела; более широкое применение мер таможенно-тарифного регулирования для защиты российского продовольственного рынка от недобросовестной конкуренции со стороны импорта и т.п. В комментариях к «дорожной карте» прозвучали слова о необходимости инвестиций и действенной поддержки отечественных производителей, кредитных программ с продленными сроками и низкими процентами и др. Возникает естественный вопрос – сколько понадобится инвестиций, чтобы реализовать «дорожную карту»? Для этого можно воспользоваться оптимизационной двухкритериальной экономико-математической задачей, решение которой, как нам представляется, может дать ответ на поставленный вопрос. Известно, что существует множество экономических задач, имеющих несколько целей, не сводимых в один критерий (например, стоимость и надежность, производительность и экология и др.), но, тем не менее, требуется найти решение, приводящее к экстремальным значениям все эти критерии. Весьма подробно о многокритериальной оптимизации написано Р. Штойером [4].

В качестве информационной базы для решения задачи воспользуемся данными Стратегии развития пищевой и перерабатывающей промышленности России до 2020 г. [5], утвержденной, как известно, еще до событий 2014 г. Отметим, в Стратегии предусматривается, что продовольственная безопасность будет достигнута при доведении к 2020 году «доли российского производства (с учетом переходящих запасов) в общем объеме потребления:

· сахара – до 96,7%;

· растительного масла – до 84%;

· мяса и мясопродуктов – до 88,3%;

· пищевых рыбных товаров – до 82%;

· молока и молокопродуктов – до 85,3%» [4].

То есть «дорожная карта» ужесточила параметры внутреннего рынка продовольствия.

Задача анализа возможностей реализации Стратегии развития пищевой и перерабатывающей промышленности в условиях импортозамещения и новых ориентиров функционирования отрасли может быть сформулирована следующим образом – найти максимальные объемы производства основных видов продовольственных товаров, которые могут быть обеспечены минимально возможным объемом инвестиций при заданном покрытии внутреннего потребления [1].

Для формализованной записи задачи в общем виде введем обозначения:

iиндекс вида производства, ;

капиталоёмкость i-го вида производства, руб./т, ;

средняя цена единицы продукции i-го вида производства, ;

объем производства i-го вида в натуральном выражении, ;

объем инвестиций в i-й вид производства, ;

, соответственно верхняя и нижняя границы объема инвестиций в i-й вид производства, ;

суммарный объем инвестиций в развитие пищевой и перерабатывающей промышленности;

верхняя граница стоимостных объёмов по каждому виду производства.

Необходимо найти такие объемы , при которых

(1)

– суммарный объем производства в целом по отрасли в стоимостном выражении достигает максимума при следующих условиях:

(2)

– объемы инвестиций в каждый вид производства должны находиться в заданных границах;

(3)

– суммарный объем инвестиций в пищевую и перерабатывающую промышленность не должен превышать заданной величины, например, при 100 %-ом внутреннем потреблении собственных товаров всех видов;

(4)

– суммарный объем инвестиций в развитие отрасли в целом достигает минимума при следующих условиях:

(5)

– объемы производства по каждому виду производства в стоимостном выражении не должны быть ниже заданных величин;

(6)

– условие неотрицательности переменных задачи.

Отметим, что задача (1)–(6) является двухкритериальной задачей оптимизации. Для решения поставленной задачи были рассчитаны капиталоемкость по всем видам производств. При этом инвестиции по каждому виду производств, соответствующие оптимизированным объемам производства, должны были находиться в заданных пределах, нижняя граница которого была равна инвестициям по Стратегии, а верхняя соответствовала объемам при заданной доле российской продукции в потреблении.

Для реализации построенной задачи двухкритериальной оптимизации можно использовать способ преобразования целевых функций в ограничения, который является некоторой вариацией метода изменения ограничений (). В классическом виде этот метод (в англоязычной литературе – ε constrained method или ε-constraint approach) – применяется для решения разнообразных многокритериальных задач. Поисковик Google выявил более 500 тыс. англоязычных источников, в которых описывается применение этого метода при решении экономических задач. Значительное количество задач связано с эколого-экономическими проблемами. Так, в работе Norouzi М., Ahmadi А., Sharaf А., Nezhad А. [6] описывается задача оптимизации функционирования трех теплоэлектростанций, которая моделируется как задача с двумя целевыми функциями – минимизацией затрат на топливо и минимизацией выбросов в атмосферу загрязняющих веществ. Задача решается с помощью сочетания лексикографической оптимизации и метода ε-ограничений.

В работе Yue D., You F. [7] рассматривается проблема календарного планирования с точки зрения двух целей – достижения максимальной прибыли при одновременной минимизации экологических нарушений. Задача в частности реализуется с помощью метода ε-ограничений. Двухкритериальным эколого-экономическим задачам, реализуемым с помощью этого же метода, посвящены работы Svensson Е. и Berntsson Т. [8], Slivinsky M, Yue D. [9]. Eshwihdi A. [10] использовал метод ε-ограничений при разработке гидро-экономического симулятора, предназначенного для совершенствования управления водными ресурсами в бассейне реки Нил.

Среди русскоязычных публикаций можно отметить работу группы авторов из Центрального экономико-математического института РАН [11], в которой метод ε-ограничений был адаптирован для процесса подготовки вариантов инвестиционных программ применительно к химической и нефтегазохимической отраслям. Ю.А. Сорокин [12] использовал метод ε-ограничений при решении оптимизационных эколого-экономических многокритериальных задач, связанных с использованием в холодильной промышленности озоноразрушающих веществ.

Метод изменения ограничений (ε-ограничений) состоит в следующем: одну из целевых функций оставляют в качестве целевой, а остальные превращают в ограничения. То есть, пусть будет целевой, а остальные представим как ограничение неравенства:

при условиях

, , (7)

Значения могут рассматриваться как допустимые уровни для .

Мы же будем действовать следующим образом. Сначала найдём по отдельности оптимальные значения целевых функций и при исходных ограничениях задачи:

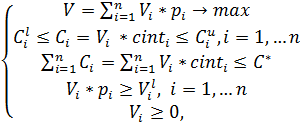(8)

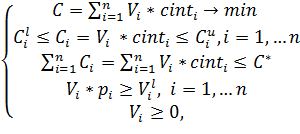(9)

Получим оптимальные значения критериев эффективности и путем решения задач линейной оптимизации (2) и (3) соответственно.

Введем новую переменную – относительное значение экономических показателей.

Теперь преобразуем критерии эффективности в безразмерные ограничения (дополнительные ограничения):

(10)

Далее конструируем новую задачу относительно переменных ,:

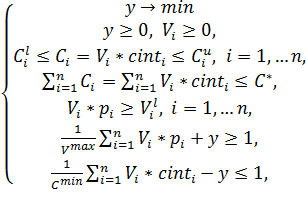(11)

В итоге получаем задачу линейного программирования (11), решением которой является – мерный вектор .

Смысл этого вектора состоит в том, что мы нашли оптимальные объемы производства, которые дают нам максимально возможный выпуск продукции при минимальных инвестициях удовлетворяющих заданным изначально ограничениям. Значение переменной состоит в том, что она выражает меру отклонения от оптимальных значений критериев, вычисленных независимо друг от друга. Минимизация позволяет определить некоторую гармоничную точку, лежащую между и , удовлетворяющую теперь всем ограничениям модели одновременно.

Для решения задачи потребовалось рассчитать коэффициенты капиталоотдачи, которые отражают эффективность использования капитала. Определяется этот коэффициент отношением объема произведенной за определенное время продукции к сумме капитальных вложений. Также были рассчитаны коэффициенты капиталоемкости, показатели обратные капиталоотдаче.

В результате решения определились следующие значения инвестиций в реализацию Стратегии развития пищевой и перерабатывающей промышленности до 2020 г.:

- суммарная величина инвестиций за 2013–2020 гг., предусмотренная в Стратегии – 759,4 млрд руб.;

- суммарная величина инвестиций за 2013–2020 гг., в условиях реализации «дорожной карты» импортозамещения – 772,4 млрд руб.;

- суммарная величина инвестиций за 2013–2020 гг., при 100% насыщения внутреннего рынка за счет собственного производства продовольственных продуктов – 777,8 млрд руб.

Конечно, решения двухкритериальной задачи, основанной на данных Стратегии, носит условный характер. Тем не менее, при корректной постановке, например, с детализацией видов продовольствия и с включением сельского хозяйства в условия и ограничения задачи, такой способ определения необходимых инвестиций в развитие отечественной продовольственной базы может дать приемлемые результаты.

[1] совместно с Веригиным Т.Ю.