Качество управления паевыми инвестиционными фондами РФ: комплексная оценка
Олькова А.Е.1
1 Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации
Скачать PDF | Загрузок: 10
Статья в журнале
Глобальные рынки и финансовый инжиниринг *
Том 3, Номер 1 (Январь-Март 2016)
* Этот журнал не выпускается в Первом экономическом издательстве
Цитировать:
Олькова А.Е. Качество управления паевыми инвестиционными фондами РФ: комплексная оценка // Глобальные рынки и финансовый инжиниринг. – 2016. – Том 3. – № 1. – С. 39-66. – doi: 10.18334/grfi.3.1.37064.
Аннотация:
В статье оценивается качество управления российскими паевыми инвестиционными фондами на основании сравнения с нормативным портфелем. Построена эффективная граница портфеля для случая «наивного» индексного инвестирования, оценена зависимость качества управления портфелем фонда от категории фонда. Проведена декомпозиция факторов, влияющих на комплексную оценку качества управления фондом.
Ключевые слова: качество управления, паевые инвестиционные фонды, эффективная граница портфеля, индексное инвестирование, маркет-тайминг, активное управление
JEL-классификация: C13, G12, G11
В издательстве открыта вакансия ответственного редактора научного журнала с возможностью удаленной работы
Подробнее...
Введение
Под качеством управления в наиболее общем виде понимается соответствие фактических итогов управления поставленным целям [1; С. 869]. Основной целью управления портфелем ценных бумаг является достижение максимальной доходности при принятии определенного уровня риска, который обычно задается инвестиционным регламентом фонда. Таким образом, целесообразно полагать, что оценка качества управления портфелем ценных бумаг инвестиционного фонда должна быть основана либо на соотношении доходности и риска (как в показателях, аналогичных коэффициенту Шарпа [2, 3, 4]), либо в сравнении доходности с неким нормативным значением [5, 6].
Недостатком первого метода оценки является то, что качество управления можно оценить только в сравнении с другими паевыми инвестиционными фондами, тогда как в определенных случаях возникает необходимость не в сравнительной, а в абсолютной оценке [2, 7]. Поэтому для целей данной работы мы будем пользоваться методом сопоставления средней (ожидаемой) доходности фонда с нормативным значением.
В теории в качестве ориентира для оценки качества управления используется эффективная граница портфеля [8], показывающая максимально возможную доходность при данном уровне риска. Таким образом, качество управления конкретным фондом оценивается по удаленности ожидаемой доходности от максимально возможного значения [5]. Однако на практике построение эффективной границы портфеля представляется сложной задачей, поскольку требует сбора очень большого количества информации (фактически необходимы сведения о доходности всех ценных бумаг за достаточно долгий промежуток времени). В связи с этим для целей данного исследования будет построена граница доходности некого референсного портфеля, составленного при условии «наивного» инвестирования. Под «наивной» мы понимаем стратегию инвестирования, основанную на публично доступной информации и предполагающую вложение средств в индексные портфели акций (российских и зарубежных) и облигаций, банковские депозиты, а также в валюту и активы товарного рынка в определенных пропорциях. Эффективная граница портфеля была оценена для трех случаев: инвестирование только в российские ценные бумаги и депозиты; инвестирование в российские ценные бумаги, депозиты и валютные активы; инвестирование в ценные бумаги (российские и зарубежные), депозиты и активы товарного рынка (драгоценные металлы).
Статистические характеристики доходности паевых инвестиционных фондов РФ
Качество управления паевыми инвестиционными фондами в РФ будет оцениваться по выборке из 255 открытых паевых инвестиционных фондов с достаточной историей функционирования. На предварительном этапе для всех фондов выборки по историческим значениям доходности за месяц были оценены характеристики распределения доходности фондов – среднемесячная доходность, волатильность, асимметрия и эксцесс. Полученные данные были усреднены в разрезе категорий фондов. Для целей анализа интересен также показатель размаха вариации, характеризующий неоднородность фондов по определяемому показателю в группе (таблица 1).
Таблица 1
Статистические характеристики доходности фондов в разрезе категорий
|
Категория
|
Количество фондов
|
Среднемесячная доходность
|
Волатильность (п. п.)
|
Асимметрия
|
Эксцесс
| ||||
|
Значения показателей в группе*
| |||||||||
|
акций
|
110
|
0,96 %
|
9,74
|
-0,60
|
3,86
| ||||
|
-0,35 %
|
2,00 %
|
4,82
|
13,64
|
-1,98
|
1,71
|
0,15
|
13,15
| ||
|
2,36 %
|
8,83
|
3,69
|
13,00
| ||||||
|
денежного рынка
|
4
|
0,67 %
|
1,01
|
-0,95
|
9,59
| ||||
|
0,31 %
|
0,89 %
|
0,33
|
2,66
|
-3,16
|
0,19
|
0,46
|
30,71
| ||
|
0,57 %
|
2,32
|
3,35
|
30,25
| ||||||
|
индексный
|
22
|
1,01 %
|
9,94
|
-0,74
|
3,53
| ||||
|
-0,36 %
|
1,74 %
|
8,95
|
12,45
|
-1,06
|
-0,07
|
2,67
|
4,99
| ||
|
2,10 %
|
3,50
|
0,99
|
2,32
| ||||||
|
облигаций
|
47
|
0,65 %
|
3,24
|
-1,69
|
14,69
| ||||
|
-0,62 %
|
1,24 %
|
1,00
|
10,53
|
-6,47
|
3,68
|
1,55
|
45,32
| ||
|
1,87 %
|
9,52
|
10,16
|
43,78
| ||||||
|
смешанный
|
62
|
0,76 %
|
6,97
|
-0,93
|
6,83
| ||||
|
-0,65 %
|
2,5 1%
|
2,23
|
17,08
|
-2,48
|
6,28
|
1,44
|
40,59
| ||
|
3,16 %
|
14,85
|
8,76
|
39,15
| ||||||
|
фондов
|
10
|
0,57 %
|
8,35
|
-0,76
|
6,62
| ||||
|
-1,01 %
|
1,64 %
|
3,92
|
14,39
|
-2,50
|
1,28
|
1,36
|
17,06
| ||
|
2,65 %
|
10,47
|
3,78
|
15,70
| ||||||
Источник: расчеты автора на основании данных [9]
Из таблицы 1 видно, что в среднем наиболее высокие показатели доходности наблюдаются у индексных фондов, наиболее низкие – у фондов фондов. Наименьшее значение в выборке принадлежит фонду фондов (-1,01 % / мес.), наибольшее – фонду смешанных инвестиций (2,51 % / мес.). Размах вариации максимален для выборки фондов смешанных инвестиций (3,16 п. п.), что свидетельствует о неоднородности фондов внутри данной группы. Далее в порядке убывания следуют фонды фондов, акций, индексные, облигаций и денежного рынка.
С точки зрения волатильности результаты выглядят ожидаемо: в среднем самая низкая волатильность наблюдается у фондов денежного рынка, далее в порядке возрастания следуют фонды облигаций, фонды смешанных инвестиций, фонды фондов, фонды акций и индексные фонды. Размах вариации максимален для фондов смешанных инвестиций, далее следуют фонды фондов, облигаций и акций. Наиболее однородны с точки зрения риска фонды денежного рынка и индексные фонды.
Показатели асимметрии и эксцесса также важны для целей анализа, поскольку на современном этапе доходность инвестиционных фондов распределена зачастую по законам, отличным от нормального. Среднее значение асимметрии для всех групп оказалось отрицательным. Это означает, что типичная форма распределения доходности имеет тяжелый левый «хвост» распределения. Такая форма характерна для подавляющего большинства фондов: 229 фондов из 255 демонстрируют отрицательную асимметрию. Наиболее ярко выраженная асимметрия характерна для фондов с низким уровнем риска – фондов облигаций, денежного рынка, а также смешанных инвестиций. Размах вариации максимален для фондов облигаций и фондов смешанных инвестиций, что свидетельствует о неоднородности фондов внутри данных групп. Самая однородная группа по показателю асимметрии – индексные фонды.
Показатели эксцесса, характеризующие сконцентрированность значений вокруг пика, максимальны для фондов облигаций и денежного рынка и минимальны для индексных фондов. Наиболее неоднородны внутри группы фонды облигаций, смешанных инвестиций и денежного рынка, наиболее однородны индексные фонды. При этом во всех группах наблюдается положительный эксцесс, что свидетельствует о сосредоточенности данных вокруг моды и, вероятно, «толстых хвостах».
Для оценки статистической значимости разбиения фондов на группы по категориям была построена регрессионная cross-sectional модель на фиктивные переменные, характеризующие разбиение фондов по категориям. Ниже представлены коэффициенты оцененной модели регрессии (эталонная переменная – индексные фонды).
Таблица 2
Коэффициенты регрессии основных статистических параметров на фиктивные переменные
|
|
Среднемесячная доходность
|
Волатильность (п. п.)
|
Асимметрия
|
Эксцесс
|
|
Коэффициенты регрессии на
фиктивные переменные
(статистически значимые на уровне 0,05 помечены «*») | ||||
|
C
|
0,01005*
|
0,099388*
|
-0,74314*
|
3,528106*
|
|
STOCK
|
-0,00045
|
-0,00195
|
0,146312
|
0,328448
|
|
MONEY
|
-0,00334
|
-0,08931*
|
-0,20736
|
6,060015*
|
|
BOND
|
-0,00352*
|
-0,06702*
|
-0,94274*
|
11,16059*
|
|
MIXED
|
-0,00249
|
-0,02966*
|
-0,19123
|
3,29831*
|
|
FUND
|
-0,00434*
|
-0,01593*
|
-0,01764
|
3,095639
|
|
R2
|
0,069184
|
0,678346
|
0,114635
|
0,355582
|
Из таблицы 2 видно, что в случае с волатильностью коэффициенты при всех фиктивных переменных, за исключением фондов акций, оказались значимыми. Для индексных фондов средний уровень волатильности – 9,9 п. п. Все остальные категории фондов демонстрируют более низкий уровень волатильности: фонды денежного рынка – на 8,9 п. п., фонды облигаций – на 6,7 п. п., фонды смешанных инвестиций – на 3,0 п. п., фонды фондов – на 1,6 п. п. В целом разбиение на группы по категориям объясняет 68 % вариации волатильности. Данный результат является ожидаемым, поскольку принадлежность фонда к определенной категории гарантирует определенные рисковые характеристики портфеля.
В случае со средней доходностью, асимметрией и эксцессом доходности складывается иная ситуация, чем с волатильностью. Доходность индексных фондов статистически значима и составляет в среднем около 1 % в месяц. Фонды облигаций и фондов показывают доходность ниже, чем индексные, в среднем на 0,35 и 0,43 п. п. соответственно. Коэффициенты при остальных фиктивных переменных незначимо отличны от нуля, что свидетельствует об отсутствии статистически значимых различий между доходностью индексных фондов и фондов акций, смешанных инвестиций и денежного рынка. Объясняющая способность модели низкая (6,9 %), из чего можно сделать вывод, что доходность определяется в наибольшей степени не отнесением к определенной группе (и, как следствие, не уровнем риска), а другими факторами.
В случае с асимметрией, значимым оказался только коэффициент при переменной BOND, из чего следует, что только фонды облигаций значительно отличаются от индексных по параметру асимметрии. Средняя асимметрия для индексных фондов составляет порядка -0,74, для фондов облигаций она ниже на 0,94. Объясняющая способность невелика (R2 = 0,11).
В случае с эксцессом значимыми оказались коэффициенты при переменных MONEY, BOND и MIXED, что означает, что в среднем эксцесс фондов денежного рынка, облигаций и смешанных инвестиций значительно отличается от индексных фондов. Эксцесс фондов акций и фондов значимо не отличается от индексных. Средний эксцесс индексных фондов составляет 3,53, для всех остальных категорий фондов данный показатель выше: для фондов денежного рынка – на 6,06, для фондов облигаций – на 11,16, для фондов смешанных инвестиций – на 3,30. Во всех категориях фондов, таким образом, в среднем распределение более остроконечно, чем нормальное. Объясняющая способность модели –36 %.
Построение эффективной границы референсного портфеля
В качестве базы для построения эффективной границы портфеля в качестве индикаторов доходности российских ценных бумаг были взяты ежемесячные значения следующих индексов: ММВБ, RGBITR, CBITR; – в качестве доходности банковских депозитов – среднемесячная ставка MIBID на срок от 181 дня до 1 года; в качестве индикаторов доходности вложений в иностранной валюте – индекс S&P Global 1200 и курсы доллара и евро (в качестве самостоятельных инструментов вложений), в качестве индикаторов товарного рынка – учетные цены на основные драгоценные металлы (золото, серебро, платина и палладий). Данные представлены за период с 2004 по 2015 г. Описательная статистика и матрица корреляции доходности представленных инструментов приведена ниже.
Из таблицы 3 видно, что самыми рискованными являются вложения в драгоценные металлы, далее следуют российские акции, зарубежные акции, иностранная валюта, облигации (государственные и корпоративные) и банковские депозиты. При этом самая низкая среднемесячная доходность наблюдается у валюты, далее следуют банковские депозиты и облигации, зарубежные акции, российские акции и драгоценные металлы. Наблюдается ярко выраженное отклонение среднемесячной доходности от нормального распределения: практически все инструменты (за исключением серебра) демонстрируют асимметрию и эксцесс, значимые по критерию Харке-Бера. Интересно отметить, что у российских ценных бумаг (акций и облигаций), в отличие от всех прочих инструментов, асимметрия является отрицательной, т. е. мода распределения смещена вправо, а вероятность появления значений ниже среднего выше. Эксцесс для всех значений положительный, что свидетельствует о наличии «толстых хвостов» распределения.
Таблица 3
Описательная статистика доходности используемых инструментов инвестирования
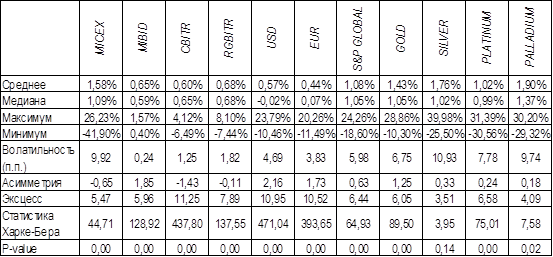
Источник: расчеты автора на основании данных [10–12]
Как видно из таблицы 4, в основном корреляция между различными инструментами инвестирования является низкой. Самая высокая корреляция наблюдается между различными драгоценными металлами, а также, по понятным причинам, между валютой и иностранными активами. В остальном низкий уровень корреляции между инструментами позволяет совместное их использование для целей диверсификации портфеля.
Таблица 4
Матрица корреляции доходности инвестиционных инструментов портфеля
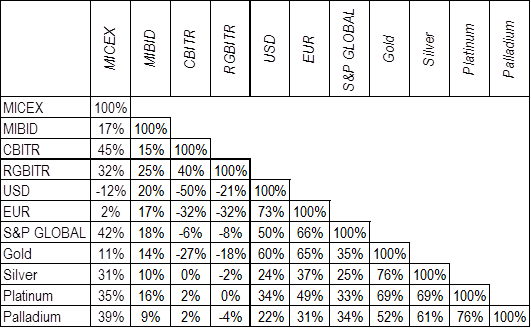
Источник: расчеты автора на основании данных [10–12]
Построение эффективной границы портфеля производилось численными методами. При заданном уровне волатильности и при известном векторе значений ожидаемой доходности и матрице ковариации подбирался вектор весов инструментов портфеля, чтобы обеспечить максимальную доходность. Оптимизационная задача в этом случае выглядит следующим образом (формула 1):
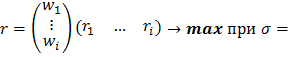
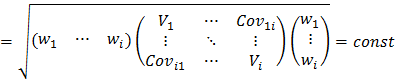 (1)
(1)
Таким образом, были получены 3 варианта эффективной границы (с инвестированием только в российские активы, в российские и иностранные активы и во все активы, включая товарный рынок).
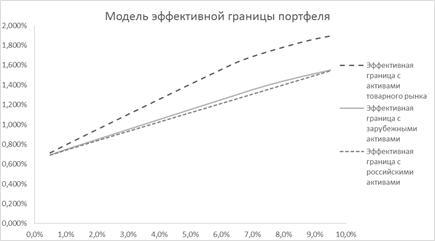
Рисунок 1. Модель эффективной границы портфеля для «наивного» инвестора
Источник: построения автора на основании данных [10–12]
Как видно из рисунка 1, включение в портфель иностранных активов незначительно влияет на потенциально возможную доходность референсного портфеля. Включение в портфель драгоценных металлов, напротив, позволяет значительно повысить ожидаемую доходность портфеля при неизменном уровне риска. В дальнейшем за основу для сравнения мы будем брать именно портфель, содержащий активы товарного рынка.
Структура оптимального портфеля при разных значениях волатильности представлена в таблице 3.
Как видно из таблицы 3, в референсный портфель не вошли такие активы, как валюта, иностранные акции и платина. Наименее рисковые активы содержат большую долю банковских депозитов, а также небольшую долю государственных облигаций, акций российских компаний, золота и палладия для целей диверсификации и повышения доходности. В портфелях со средним уровнем риска примерно в равных долях присутствуют акции, государственные облигации, золото и палладий. Портфель с наименьшим уровнем риска (волатильность 0,25 п. п. в месяц, что соответствует 0,87 п. п. в год) имеет ожидаемую доходность в размере 0,654 % / мес. (7,8 % годовых) и состоит практически целиком из активов денежного рынка (банковских депозитов) с добавлением небольшого объема корпоративных облигаций. В наиболее рисковых портфелях присутствуют в основном активы товарного рынка – золото, серебро и палладий. Портфель с наиболее высоким уровнем риска (волатильность 9,7 п. п. / мес., что соответствует 33,6 п. п. в год) состоит целиком из вложений в палладий и имеет ожидаемую доходность 1,905 % / мес. (22,9 % годовых). Более высокий уровень доходности в рамках данных предположений получить не удается.
Таблица 5
Структура референсного портфеля при различных значениях волатильности
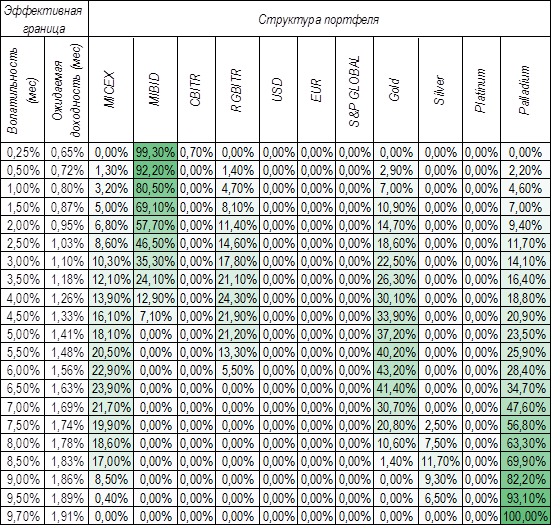
Источник: расчеты автора на основании данных [10–12]
В случае, если доступ к активам товарного рынка отсутствует, референсный портфель будет состоять из банковских депозитов, российских и зарубежных акций в различных пропорциях. Однако, как было показано ранее, подобный портфель имеет значительно более низкую ожидаемую доходность, особенно при высокой волатильности. Если отсутствует доступ и к зарубежным инструментам инвестирования, референсный портфель будет состоять целиком из российских акций и активов денежного рынка. Введение в портфель иностранных активов несущественно увеличивает доходность референсного портфеля.
При помощи полиномиального сглаживания нами было получено уравнение эффективной границы портфеля «наивного» инвестора (с использованием всех инструментов инвестирования, включая драгоценные металлы):
![]() (2)
(2)
Свободный член в уравнении эффективной границы можно трактовать как нормативную доходность безрискового портфеля. Исходя из расчетов, она должна составлять порядка 0,6 % в месяц (7,2 % годовых). С ростом уровня риска ожидаемая доходность портфеля растет, однако более медленными темпами, нежели линейная функция. Квадратичная функциональная форма свидетельствует о том, что при определенном уровне волатильности (в данном случае равном 17,1 п. п.) доходность портфеля достигает максимума и не может быть увеличена за счет более рискованных вложений.
Комплексная оценка качества управления паевыми инвестиционными фондами в РФ
В качестве комплексного показателя качества управления был использован разрыв между фактической среднемесячной доходностью фонда и доходностью референсного портфеля с аналогичной волатильностью, составленного по описанной выше методике.
Графически качество управления фонда можно представить как положение фонда в координатах «доходность–волатильность» относительно эффективной границы. Если фонд находится выше эффективной границы, то качество управления можно признать высоким, поскольку действия управляющего позволили получать доходность выше, чем при использовании «наивной» стратегии. Нахождение фонда в районе построенной эффективной границы может расцениваться как удовлетворительный результат. Если доходность фонда значительно ниже референсной, качество управления следует признавать низким.
Ниже представлена карта паевых инвестиционных фондов в координатах «доходность–волатильность» в сравнении с референсным портфелем (эффективной границей).
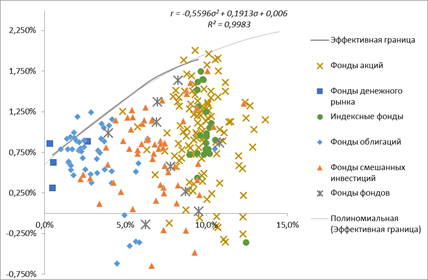
Рисунок 2. Параметры портфелей паевых инвестиционных фондов в РФ и эффективная граница портфеля
Источник: построения автора на основании данных [9–12]
Как видно из рисунка 2, качество управления паевыми инвестиционными фондами в РФ в среднем находится на достаточно низком уровне. Отставание от референсного портфеля составляет в среднем 0,85 п. п. в месяц (10,2 п. п. в год), что нельзя объяснить наличием трансакционных издержек при управлении средствами фондов.
При
разбиении фондов на группы по категориям выявлено, что отставание от
референсного портфеля статистически значимо различается для разных категорий
фондов. Для тестирования данной гипотезы был проведен анализ ANOVA, в результате которого
гипотеза о статистической незначимости разбиения на группы была отвергнута. Для уточнения
характера связи между отставанием от референсного портфеля и категорией фонда
была оценена модель регрессии переменной ![]() на фиктивные переменные, характеризующие принадлежность фонда
к определенной категории (в качестве эталонной переменной принимались
индексные фонды). Результаты проведенного анализа представлены в таблице.
на фиктивные переменные, характеризующие принадлежность фонда
к определенной категории (в качестве эталонной переменной принимались
индексные фонды). Результаты проведенного анализа представлены в таблице.
В таблице 4 приведены средние значения отставания доходности фонда от референсного портфеля. Наиболее сильное отставание наблюдается у фондов фондов – порядка 1,2 п. п. в месяц. Самое малое отставание у фондов денежного рынка – 0,1 п. п. в месяц.
Таблица 6
Анализ зависимости качества управления фондом от инвестиционной декларации фондов
|
ANOVA
| |||||||||||
|
Категории
|
Количество
фондов в выборке
|
Среднее
значение отставания доходности фонда
от референсного портфеля
| |||||||||
|
акций
|
110
|
-0,00960
| |||||||||
|
денежного рынка
|
4
|
-0,00111
| |||||||||
|
индексный
|
22
|
-0,00941
| |||||||||
|
облигаций
|
47
|
-0,00491
| |||||||||
|
смешанный
|
62
|
-0,00874
| |||||||||
|
фондов
|
10
|
-0,01195
| |||||||||
|
Источник
вариации
|
SS
|
df
|
MS
|
F
|
P-Значение
| ||||||
|
Между группами
|
0,0011
|
5
|
0,00022
|
6,82
|
0,00001
| ||||||
|
Внутри групп
|
0,008
|
249
|
0,00003
| ||||||||
|
Итого
|
0,0091
|
254
|
|
|
| ||||||
|
Регрессия
на фиктивные переменные
| |||||||||||
|
Dependent Variable: PERFORMANCE
| |||||||||||
|
Method: Least Squares
| |||||||||||
|
Date: 12/20/15 Time: 00:21
| |||||||||||
|
Sample: 1 255
| |||||||||||
|
Included observations: 255
| |||||||||||
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
| |||||||
|
C
|
-0,009411
|
0,001211
|
-7,769794
|
0,0000
| |||||||
|
STOCK
|
-0,000192
|
0,001327
|
-0,144426
|
0,8853
| |||||||
|
MONEY
|
0,008304
|
0,003088
|
2,689087
|
0,0076
| |||||||
|
BOND
|
0,004504
|
0,001468
|
3,068917
|
0,0024
| |||||||
|
MIXED
|
0,000671
|
0,00141
|
0,475775
|
0,6347
| |||||||
|
FUND
|
-0,00254
|
0,002167
|
-1,1725
|
0,2421
| |||||||
|
R-squared
|
0,120376
|
Mean dependent var
|
-0,00847
| ||||||||
|
Adjusted R-squared
|
0,102713
|
S.D. dependent var
|
0,005998
| ||||||||
|
S.E. of regression
|
0,005681
|
Akaike info criterion
|
-7,48006
| ||||||||
|
Sum squared resid
|
0,008037
|
Schwarz criterion
|
-7,39674
| ||||||||
|
Log likelihood
|
959,7077
|
Hannan-Quinn criter.
|
-7,44654
| ||||||||
|
F-statistic
|
6,815089
|
|
| ||||||||
|
Prob(F-statistic)
|
0,000006
|
|
| ||||||||
Расширенный анализ методом регрессии на фиктивные переменные показывает, что качество управления фондами денежного рынка и облигаций выше, чем у прочих фондов: коэффициенты при фиктивных переменных MONEY и BOND статистически значимы и равны 0,83 п. п. и 0,45 п. п. соответственно. Это означает, что в сравнении с индексными фондами отставание по доходности от референсного портфеля меньше на соответствующее количество процентных пунктов. У прочих категорий фондов коэффициенты регрессии оказались статистически незначимыми. В целом объясняющая способность модели невысока (R2 = 0,12), поэтому можно констатировать, что качество управления фондом зависит в значительной степени от прочих факторов.
Компоненты качества управления паевыми инвестиционными фондами в РФ
По нашему мнению, качество управления портфеля складывается из следующих компонентов:
1. Способность удачно отбирать активы для инвестирования.
2. Способность к диверсификации портфеля.
3. Способность к маркет-таймингу.
Далее в отдельности будет рассмотрен каждый из описанных факторов.
Способность отбора активов
Качество управления портфелем зависит от того, насколько менеджер портфеля в состоянии идентифицировать бумаги с благоприятными перспективами роста. Высокое качество управления достигается тогда, когда сформированный портфель показывает доходность по крайней мере не ниже, чем среднерыночная (с учетом присущего фонду уровня риска).
Традиционно данный фактор оценивается через показатель «альфа», выведенный из уравнения CAPM. Экономический смысл показателя «альфа» из приведенного выше уравнения заключается в средней величине превышения доходности фонда над среднерыночной доходностью, скорректированной на уровень присущего фонду риска.
Однако подобная методика не лишена недостатков. В частности, поскольку объект инвестирования для большинства фондов определяется заранее и предусмотрен инвестиционной декларацией, превышение доходности над среднерыночной с учетом риска может быть связано не столько с активными действиями управляющего по поиску инструментов инвестирования, сколько с благоприятной ситуацией на рынке соответствующего инструмента. Для устранения этого фактора используется показатель «стилевой альфы» (style alpha), где в уравнении CAPM вместо единственного бенчмарка подставляется индекс, соответствующий выбранной инвестиционной декларации (например, индекс облигаций, индекс акций, композитный индекс, характерный для смешанного портфеля акций и облигаций и др.). В рамках данного исследования мы оцениваем как альфу для случая единственного бенчмарка, так и стилевую альфу. В качестве стилевых бенчмарков были использованы следующие индексные портфели:
- Портфель, состоящий из акций (Индекс ММВБ).
- Портфель, состоящий из иностранных ценных бумаг (Индекс S&P Global 1200).
- Портфель, состоящий из государственных облигаций (Индекс RGBITR).
- Портфель, состоящий из корпоративных облигаций (Индекс CBITR).
- Портфель, состоящий на 57,9 % из корпоративных облигаций и на 42,1% – из государственных (взвешенная комбинация индексов CBITR и RGBITR).
- Портфель, состоящий на 68,3 % из акций, на 18,4 % – из корпоративных облигаций, на 13,4 % – из государственных облигаций (взвешенная комбинация индексов ММВБ, CBITR, RGBITR) [1].
- Ставка MIBID (в качестве бенчмарка доходности депозитов финансовых институтов).
- Золото.
В качестве предпосылки принимается, что вложение в любой портфель активов, отличный от перечисленных выше, является управленческим решением по выбору инструментов инвестирования.
Для
целей данной работы в оценка показателя «альфа» мы используем не традиционное
уравнение CAPM, а упрощенное, вида ![]() . Достоинством данного уравнения является, во‑первых,
отсутствие необходимости введения безрисковой ставки в модель, во-вторых,
простота экономической трактовки.
. Достоинством данного уравнения является, во‑первых,
отсутствие необходимости введения безрисковой ставки в модель, во-вторых,
простота экономической трактовки.
Следует отметить, что при оценивании описанной выше модели (как для единственного бенчмарка, так и для стилевых бенчмарков) в подавляющем большинстве случаев коэффициент «альфа» оказался статистически незначимым, а коэффициент «бета» – статистически значимым. Незначимость коэффициента «альфа» связана с большой стандартной ошибкой оценки. Этот факт обусловлен тем, что превышение доходности над рыночной за рассматриваемый период было нестабильным.
Средние значения показателей «альфа» и «стилевая альфа» представлены в таблице 7.
Таблица 7
Средние значения показателей «альфа» и «стилевая альфа» по категориям фондов
|
Категории фондов
|
Среднее значение
показателя «альфа»
|
Среднее значение стилевой
альфы
|
|
акций
|
0,00028
|
0,00032
|
|
денежного рынка
|
0,00616
|
0,00057
|
|
индексный
|
-0,00001
|
-0,00001
|
|
облигаций
|
0,00420
|
0,00019
|
|
смешанный
|
-0,00010
|
-0,00150
|
|
фондов
|
0,00021
|
-0,00198
|
|
Fстат.
|
6,74
|
1,35
|
|
P-value
|
0,000006
|
0,243327
|
Как видно из таблицы 7, недостаток модели с единственным бенчмарком, описанный выше, является существенным для данной выборки – различия по категориям являются статистически значимыми по F-критерию. Фонды денежного рынка и облигаций в среднем показывают существенно более высокий коэффициент «альфа», чем фонды других категорий, что можно объяснить более благоприятной ситуацией на данных рынках в рассматриваемом периоде. При использовании стилевого подхода этот недостаток исчезает: для показателя «стилевая альфа» различия по категориям статистически незначимы по F-критерию.
С точки зрения стилевого подхода самый низкий по модулю показатель принадлежит индексным фондам, что обусловлено пассивным характером управления. Отрицательная стилевая альфа характерна для фондов смешанных инвестиций и фондов, небольшая положительная стилевая альфа – для фондов денежного рынка, акций и облигаций. Наибольшее значение стилевой альфы характерно для фондов денежного рынка. Это может быть обусловлено тем, что ставки, предлагаемые банками по депозитам паевых фондов, выше, чем ставка MIBID, принимаемая в качестве бенчмарка.
Способность к диверсификации портфеля
Уровень диверсификации портфеля можно оценить через показатель несистематического риска. Несистематический риск – это ошибка регрессии в уравнении CAPM, описанном выше. При этом можно рассматривать, как и в предыдущем случае, уравнение с единственным бенчмарком либо уравнение со стилевыми бенчмарками. Ниже представлены результаты оценки несистематического риска для обоих случаев.
Таблица 8
Средние значения показателей несистематического риска по категориям фондов
|
Группы
|
Среднее значение
несистематического риска (модель с одним бенчмарком)
|
Среднее значение
несистематического риска (модель со стилевыми бенчмарками)
|
|
акций
|
0,047532
|
0,048808
|
|
денежного рынка
|
0,009173
|
0,009722
|
|
индексный
|
0,022921
|
0,022921
|
|
облигаций
|
0,025719
|
0,02832
|
|
смешанный
|
0,036424
|
0,036802
|
|
фондов
|
0,058038
|
0,065148
|
|
Fстат.
|
17,9
|
16,7
|
|
P-value
|
0,000000
|
0,000000
|
Как видно из таблицы 8, в обоих случаях показатели несистематического риска значительно различаются в зависимости от категорий фондов. При этом для разных оцененных уравнений показатели различаются несущественно. Наиболее низкий уровень несистематического риска в среднем отмечается у фондов денежного рынка, что может быть объяснено общим низким уровнем риска данного типа фондов. Далее по нарастающей следуют индексные фонды, фонды облигаций, смешанных инвестиций, акций, фондов. Таким образом, наиболее диверсифицированными являются портфели индексных фондов, наименее – фондов фондов. Деление по группам значимо по F-критерию.
Способность к маркет-таймингу
Способность к маркет-таймингу (выбору времени для купли-продажи активов) мы оцениваем через показатели коасимметрии доходности фонда с доходностью бенчмарка. Наличие положительной коасимметрии свидетельствует о том, что реакция фонда на улучшение конъюнктуры рынка (финансового рынка в целом или рынка соответствующего инструмента) проявляется сильнее, чем на ее ухудшение (т. е. зависимость на левом «хвосте» распределения отличается от зависимости на правом «хвосте»). Наличие положительного коэксцесса свидетельствует о том, что реакция фонда на любые экстремальные события (улучшение или ухудшение конъюнктуры) повышенная по сравнению с нормальным значением (т. е. зависимость на «хвостах» распределения отличается от зависимости вблизи центральных значений). Таким образом, способность к маркет-таймингу тем лучше, чем больше значение коасимметрии и чем меньше значение коэксцесса. Как и в предыдущих случаях, можно оценивать данные показатели для случая единственного бенчмарка и для случая стилевых бенчмарков.
Таблица 9
Средние значения показателей коасимметрии по категориям фондов
|
Группы
|
Средняя коасимметрия к единственному
бенчмарку
|
Средняя коасимметрия к
стилевым бенчмаркам
|
|
акций
|
-0,79595
|
-0,74526
|
|
денежного рынка
|
-0,3651
|
0,68132
|
|
индексный
|
-0,90241
|
-0,90241
|
|
облигаций
|
-0,78185
|
-0,92352
|
|
смешанный
|
-0,85053
|
-0,8615
|
|
фондов
|
-0,83173
|
-0,0944
|
|
Fстат.
|
3,28232
|
16,65861
|
|
P-value
|
0,006877
|
0,000000
|
Как видно из таблицы 9, коасимметрия к единственному бенчмарку для всех категорий фондов в среднем отрицательная. Коасимметрия к стилевым бенчмаркам положительная только для фондов денежного рынка. Это свидетельствует в целом о неудачном маркет-тайминге фондов в рассматриваемом периоде. Наилучшее качество маркет-тайминга у фондов денежного рынка, наихудшее – у индексных фондов (по сравнению с единственным бенчмарком).
Таблица 10
Средние значения показателей коэксцесса по категориям фондов
|
Группы
|
Среднее значение
коэксцесса к единственному бенчмарку
|
Среднее значение
коэксцесса к стилевым бенчмаркам
|
|
акций
|
5,288697
|
5,056511
|
|
денежного рынка
|
2,641361
|
2,14232
|
|
индексный
|
6,000183
|
6,000183
|
|
облигаций
|
4,089014
|
5,640356
|
|
смешанный
|
5,327018
|
5,398358
|
|
фондов
|
4,608991
|
2,233621
|
|
Fстат.
|
16,9
|
6,9
|
|
P-value
|
0,000000
|
0,000005
|
Как видно из таблицы 10, самые низкие значения коэксцесса характерны для фондов денежного рынка, самые высокие – для индексных фондов. Значения коэксцесса во всех категориях положительные, что свидетельствует о низком качестве управления в целом. Различия по группам статистически значимы по F-критерию в обоих случаях.
Факторный анализ качества управления паевыми инвестиционными фондами в РФ
Для
выявления значимости воздействия каждого из описанных выше компонентов была
оценена регрессионная модель, в которой в качестве зависимой переменной
принимается отставание средней доходности фонда от доходности референсного портфеля
(![]() ). В качестве факторов в модель были включены следующие:
). В качестве факторов в модель были включены следующие:
- Альфа (стилевая альфа) как показатель качества отбора активов.
- Асимметрия распределения доходности фонда.
- Эксцесс распределения доходности фонда.
- Коасимметрия (стилевая коасимметрия) как показатель маркет-тайминга.
- Коэксцесс (стилевой коэксцесс) как показатель маркет-тайминга.
- Несистематический риск как показатель способности к диверсификации.
- Систематический риск (бета*стандартное отклонение бенчмарка).
- Уровень трансакционных издержек (вознаграждение УК, спец. депозитарию и аудиторам и расходы, осуществляемые за счет активов, в % к стоимости активов).
- Активный/пассивный характер управления фондом. В качестве показателя активности принимался R2 уравнения CAPM с единственным бенчмарком или стилевыми бенчмарками. Чем выше данный показатель, тем большую долю вариации доходности фонда объясняет вариация доходности индекса. Таким образом, низкое значение R2 соответствует активному управлению фондом, а высокое – пассивному (следование индексу).
В результате построения регрессионной модели уровень трансакционных издержек во всех случаях оказался статистически незначимым и исключен из модели. Фактически это означает, что наличие значимой взаимосвязи между отставанием от доходности референсного портфеля и уровнем трансакционных издержек отвергается.
Ниже представлены две модели – с использованием и без использования стилевого подхода в оценке альфы, коасимметрии и коэксцесса.
Таблица 11
Модель регрессии качества управления российскими паевыми инвестиционными фондами на нестилевые факторы
|
Dependent Variable: PERFORMANCE
| |||||||
|
Method: Least Squares
| |||||||
|
Date: 12/30/15 Time: 17:29
| |||||||
|
Sample: 1 255
| |||||||
|
Included observations: 255
| |||||||
|
White Heteroskedasticity-Consistent Standard Errors &
Covariance
| |||||||
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
| |||
|
C
|
-0,006595
|
0,000646
|
-10,215640
|
0,0000
| |||
|
ALPHA
|
0,982395
|
0,032338
|
30,378930
|
0,0000
| |||
|
SKEWNESS
|
-0,000726
|
0,000189
|
-3,845630
|
0,0002
| |||
|
SYS_RISK
|
-0,045477
|
0,012900
|
-3,525348
|
0,0005
| |||
|
UNSYS_RISK
|
-0,045827
|
0,012478
|
-3,672582
|
0,0003
| |||
|
COSKEWNESS
|
0,00554
|
0,000896
|
6,184557
|
0,0000
| |||
|
R_SQ
|
0,008598
|
0,001488
|
5,776308
|
0,0000
| |||
|
R-squared
|
0,848409
|
Mean dependent var
|
-0,00847
| ||||
|
Adjusted R-squared
|
0,844741
|
S.D. dependent var
|
0,005998
| ||||
|
S.E. of regression
|
0,002363
|
Akaike info criterion
|
-9,23052
| ||||
|
Sum squared resid
|
0,001385
|
Schwarz criterion
|
-9,13331
| ||||
|
Log likelihood
|
1183,892
|
Hannan-Quinn criter.
|
-9,19142
| ||||
|
F-statistic
|
231,3295
|
Prob(F-statistic)
|
0,000000
| ||||
Как видно из таблицы 11, модель без использования стилевых показателей позволяет объяснить 85 % вариации результирующего показателя качества управления. Показатели эксцесса и коэксцесса были исключены из модели за статистической незначимостью. Все остальные коэффициенты являются статистически значимыми. Значение константы – -0,66 п. п. в месяц, что соответствует отставанию от референсного портфеля в 7,9 п. п. в год. Данное отставание можно объяснить наличием трансакционных издержек. Наибольшее влияние на результирующий признак оказывает показатель альфа. Положительный коэффициент при данном показателе свидетельствует о прямой взаимосвязи между регрессором и зависимой переменной. Влияние прочих факторов не столь существенное, но статистически значимое.
Уровень риска (как систематического, так и несистематического) имеет обратную связь с качеством управления – эмпирически при прочих равных условиях увеличение уровня риска ведет к снижению качества управления.
Асимметрия распределения доходности связана с качеством управления обратной связью. Это свидетельствует о том, что у фондов с отрицательной асимметрией отставание от референсного портфеля в среднем меньше, чем с положительной (при прочих равных условиях). Коасимметрия как показатель маркет-тайминга связана с качеством управления прямой зависимостью – чем выше коасимметрия, тем выше качество управления.
Активность управления связана с качеством управления прямой зависимостью – чем более активно управляется фонд, тем выше качество управления.
Ниже представлена аналогичная модель, но с использованием стилевого подхода к определению альфы, коасимметрии и коэксцесса.
Таблица 12
Модель регрессии качества управления российскими паевыми инвестиционными фондами на стилевые факторы
|
Dependent Variable: PERFORMANCE
| |||||||
|
Method: Least Squares
| |||||||
|
Date: 12/30/15 Time: 17:20
| |||||||
|
Sample: 1 255
| |||||||
|
Included observations: 255
| |||||||
|
White Heteroskedasticity-Consistent Standard Errors &
Covariance
| |||||||
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
| |||
|
C
|
-0,004161
|
0,000788
|
-5,281446
|
0,0000
| |||
|
STYLE_ALPHA
|
0,901029
|
0,041460
|
21,73246
|
0,0000
| |||
|
SKEWNESS
|
-0,000634
|
0,000223
|
-2,847161
|
0,0048
| |||
|
SYS_RISK
|
-0,062137
|
0,011441
|
-5,431073
|
0,0000
| |||
|
UNSYS_RISK
|
-0,064787
|
0,012560
|
-5,158003
|
0,0000
| |||
|
COSKEW_STYLE
|
0,001391
|
0,000488
|
2,846902
|
0,0048
| |||
|
STYLE_R_SQ
|
0,004453
|
0,001382
|
3,221915
|
0,0014
| |||
|
R-squared
|
0,777252
|
Mean dependent var
|
-0,008470
| ||||
|
Adjusted R-squared
|
0,771863
|
S.D. dependent var
|
0,005998
| ||||
|
S.E. of regression
|
0,002865
|
Akaike info criterion
|
-8,845670
| ||||
|
Sum squared resid
|
0,002035
|
Schwarz criterion
|
-8,748459
| ||||
|
Log likelihood
|
1134,823
|
Hannan-Quinn criter.
|
-8,806568
| ||||
|
F-statistic
|
144,2275
|
Prob(F-statistic)
|
0,000000
| ||||
Как видно из таблицы 12, объясняющая способность модели со стилевыми факторами ниже, чем с нестилевыми (78 %), а также уступает по информационным критериям. Из этого следует, что успех паевого инвестиционного фонда связан не только с эффективностью его текущего управления, но и с выбранной инвестиционной декларацией. Определенная доля вариации качества управления объясняется выбором стилевого бенчмарка. Ранее было показано, что фонды с определенной инвестиционной декларацией (облигаций, денежного рынка) управляются в среднем лучше, чем остальные. Эксцесс был исключен из модели в связи со статистической незначимостью, а коэксцесс – в результате коллинеарности с коасимметрией. Коэффициенты при прочих факторах имеют ту же интерпретацию, что и в предыдущей модели.
Заключение
В рамках проведенного исследования были достигнуты следующие результаты.
Параметры распределения доходности фондов, относимых к различных категориям, существенно отличаются. В среднем наиболее высокие показатели ожидаемой доходности наблюдаются у индексных фондов, далее следуют фонды акций, смешанных инвестиций, денежного рынка и облигаций. Наиболее низкая средняя доходность – у фондов фондов. Наиболее неоднородными по параметру «ожидаемая доходность» являются фонды смешанных инвестиций.
Самая низкая волатильность наблюдается у фондов денежного рынка, далее в порядке возрастания следуют фонды облигаций, фонды смешанных инвестиций, фонды фондов, фонды акций и индексные фонды. Размах вариации максимален для фондов смешанных инвестиций, далее следуют фонды фондов, облигаций и акций. Наиболее однородны с точки зрения риска фонды денежного рынка и индексные фонды.
Среднее значение асимметрии для всех групп оказалось отрицательным. Это означает, что типичная форма распределения доходности имеет тяжелый левый «хвост» распределения. Наиболее ярко выраженная асимметрия характерна для фондов с низким уровнем риска – фондов облигаций, денежного рынка, а также смешанных инвестиций.
Показатели эксцесса максимальны для фондов облигаций и денежного рынка и минимальны для индексных фондов. При этом во всех группах наблюдается положительный эксцесс, что свидетельствует о сосредоточенности данных вокруг моды и, вероятно, «толстых хвостах».
В целом качество управления российскими открытыми паевыми инвестиционными фондами остается на низком уровне. За рассматриваемый период у большинства фондов наблюдается отставание от эффективной границы. Это означает, что «наивное» индексное инвестирование дает лучшие результаты, чем вложение в паевые инвестиционные фонды. При разбиении фондов на группы по категориям выявлено, что отставание от референсного портфеля статистически значимо различается для разных категорий фондов. Самое высокое качество управления характерно для фондов с низким уровнем риска – фондов облигаций и денежного рынка.
Пофакторное разложение качества управления паевыми инвестиционными фондами показало, что в наибольшей степени низкое качество управления связано с неудачным выбором активов для инвестирования. Среднегрупповые показатели стилевой альфы наиболее высоки для фондов денежного рынка, акций и облигаций. Для индексных фондов, фондов смешанных инвестиций и фондов фондов альфа является отрицательной, что свидетельствует о том, что за рассматриваемый период доходность бенчмарка, скорректированная на риск, была выше, чем у фонда.
Кроме того, статистически значимы такие факторы, как уровень систематического риска фонда и способность к диверсификации портфеля. Чем выше уровень как систематического, так и несистематического риска, тем в среднем хуже качество управления. Наиболее высокий уровень несистематического риска наблюдается у фондов фондов, смешанных инвестиций и акций.
Способность к маркет-таймингу оказывает слабое (по сравнению с другими факторами), но статистически значимое воздействие на качество управления. Качество маркет-тайминга может оцениваться как низкое для всех категорий фондов.
В среднем, более высокое качество управления наблюдается у активно управляемых фондов.
[1] Веса были рассчитаны исходя из доли соответствующего инструмента в капитализации фондового рынка (Источник: www.naufor.ru).
Источники:
2. Cogneau P., Hubner G. The 101 ways to measure portfolio performance [Electronic resource] // SSRN. – 2009. – Mode of access: http://ssrn.com/abstract=1326076
3. Sharpe W. F. The Sharpe Ratio // Journal of Portfolio Management. – 1994. – Vol. 21. – № 1. – P. 49–58.
4. Sharpe W. F. Mutual fund performance // Journal of Business. – 1966. – Vol. 39. – № 1–2. – P. 119–138.
5. Cantaluppi L., Hug R. Efficiency ratio: A new methodology for performance measurement // Journal of Investing. – 2000. – Vol. 9. – № 2. – P. 19–25.
6. Graham J. R., Harvey C. R. Grading the performance of market-timing newsletters // Financial Analysts Journal. – 1997. – Vol. 53. – № 6. – P. 54–66.
7. A survey on the four families of performance measures / M. Caporin, F. Lisi, G. M. Jannin [et al.] // Journal of Economic Surveys. – 2014. – Vol. 28. – № 5. – P. 917–942.
8. Markowitz H. Portfolio Selection. – New York: John Wiley & Sons Inc., 1959.
9. Сайт Национальной лиги управляющих.
10. Сайт Московской Биржи.
11. Официальный сайт Центрального банка Российской Федерации.
12. Standard&Poor's Agency [Electronic resource] // S&P Dow Jones Indices. – Mode of access: http://us.spindices.com/
Страница обновлена: 22.01.2024 в 21:05:11
