Инновационный подход планирования распределения продуктов питания с учетом интенсивности спроса
Тюрин А.Ю.1
1 Кузбасский государственный технический университет имени Т.Ф. Горбачева
Скачать PDF | Загрузок: 1
Статья в журнале
Вопросы инновационной экономики (РИНЦ, ВАК)
опубликовать статью | оформить подписку
Том 4, Номер 4 (Октябрь-Декабрь 2014)
Цитировать:
Тюрин А.Ю. Инновационный подход планирования распределения продуктов питания с учетом интенсивности спроса // Вопросы инновационной экономики. – 2014. – Том 4. – № 4. – С. 10-19. – doi: 10.18334/inec.4.4.297.
Эта статья проиндексирована РИНЦ, см. https://elibrary.ru/item.asp?id=24187691
Аннотация:
Рассматриваются вопросы применения двухэтапного подхода к планированию распределения хлебобулочных изделий по торговым точкам. Отмечается необходимость координации производственных и транспортных процессов с учетом ритма выпуска готовой продукции и интенсивности ее потребления. Приводится математическая модель, позволяющая получить оптимальное распределение товаров по периодам завоза. На конкретном примере на первом этапе решается задача разбивки партий поставки по периодам завоза, которые являются основой построения маршрутов перевозок на втором этапе.
Ключевые слова: распределение продукции, логистическая система, транспортные расходы, интенсивность спроса, двухэтапный подход
В издательстве открыта вакансия ответственного редактора научного журнала с возможностью удаленной работы
Подробнее...
Введение
Использование принципов логистики становится неотъемлемым фактором производственной деятельности различных предприятий и фирм, а формирование логистической системы всех участников продвижения материального потока позволяет выработать единые правила управления логистическими процессами в различных отраслях экономики. Рассмотрение цепи «поставщик-транспорт-потребитель» как логистической системы позволяет учесть интересы всех сторон, выработать компромиссное решение, удовлетворяющее всем ограничениям, и построить различные варианты маршрутов доставки продукции в зависимости от принятых критериев оптимальности [1].
Учет прямых и косвенных издержек возможен при анализе ритма выпуска готовой продукции, режимов работы сбытовых организаций производства, распределения спроса по торговым точкам в течение дня, учете тенденций изменения спроса в течение длительного периода времени и провозной способности транспортных средств [2].
Рассмотрим логистическую систему сбыта готовой продукции при производстве хлеба. Производственный процесс характеризуется относительно равномерным выпуском хлебобулочных изделий, а процесс сбыта определяется соотношением между количеством подготовленных отгрузочных партий и наличием транспортных средств. В случае ограниченного режима работы транспортных средств на складе экспедиции накапливается запас готовой продукции, который необходимо вывезти в течение небольшого периода времени. Иначе могут исчерпаться ресурсы складской площади в связи с поступлением новой продукции, в худшем случае возникнут потери из-за ограниченного срока хранения товара (до 14 ч).
Быстрое реагирование на предъявленный спрос и доставка свежей продукции позволят поддержать объем продаж на достигнутом уровне, а задержка поставки, скорее всего, приведет к оттоку части покупателей и снижению спроса в данной торговой точке. Также необходимо отметить особенности работы транспорта по доставке хлебобулочных изделий. Для больших транспортных сетей с числом потребителей более 100 задача разработки маршрута доставки является сложной даже для одного типа транспортных средств. А в сбытовых системах производства хлебобулочных изделий работает подвижной состав различной грузоподъемности и принадлежности. Поэтому возникают дополнительные задачи по выбору и распределению транспортных средств по маршрутам доставки.
Таким образом, выбор оптимальных режимов взаимодействия в сбытовых системах должен происходить с учетом технологических особенностей производства и потребления, режимов работы транспорта на основе общих логистических издержек и возможных потерь вследствие неучета рассмотренных выше факторов.
Для решения поставленной задачи предлагается двухэтапный подход. На первом этапе происходит оптимальное распределение объемов поставок по периодам завоза с учетом динамики спроса. На втором этапе под оптимальные партии поставок подбираются транспортные средства различной грузоподъемности и принадлежности и формируется график доставки хлебобулочной продукции потребителям.
Решение задачи первого этапа основано на учете всех логистических издержек и потерь, связанных с процессом сбыта. Предполагается, что общие затраты состоят из транспортных расходов по доставке оптимальных партий поставок, потерь вследствие несвоевременного удовлетворения спроса, организационных расходов по формированию партии поставки, а также возможных потерь из-за задержки вывоза ночного запаса.
На втором этапе корректируются транспортные расходы и формируются окончательные затраты на управление процессом сбыта. Так как для доставки продукции в свежем виде требуется осуществлять два-три завоза одному и тому же потребителю в течение дня, то принимаем максимальное количество поставок одному грузополучателю равным трем. На первом этапе для доставки продукции предполагается подвижной состав одной грузоподъемности, работающий по маятниковому маршруту. Таким образом, моделируется наихудший вариант транспортного обслуживания и, соответственно, наибольшие транспортные расходы.
Рассмотрим математическую постановку решения задачи распределения на первом этапе.
Как было отмечено выше, необходимо осуществить максимум три завоза одному потребителю с учетом ограничений по выпуску и потреблению продукции. Поэтому в качестве прототипа можно взять известную транспортную задачу Хичкока-Купманса с тремя складами [3] с некоторыми дополнениями.
В качестве складов в предлагаемой модели управления выступают периоды производства и реализации готовой продукции с ограничениями на выпуск.
Для определения оптимального распределения поставок по периодам завоза используем метод последовательных приближений. Так как для формирования оптимального распределения используется также модель с двумя складами, опишем ее подробней.
Математическая модель задачи
Обозначим через xij – количество готовой продукции, отправляемое от поставщика в i-й период времени в j-й пункт потребления, ед.; N- общее количество потребителей.
Тогда суммарные затраты, которые необходимо свести к минимуму, определяются из выражения
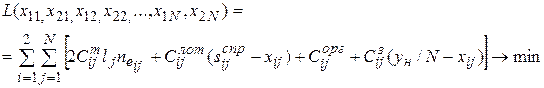 (1)
(1)
при ограничениях
![]() ;
; ![]() ;
(2)
;
(2)
![]() ;
; 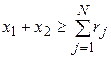 ;
; 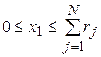 ; (3)
; (3)
где ![]() - транспортные расходы по доставке
продукции на расстояние lj от
поставщика в i-й
период времени в j-й
пункт потребления, р./км;
- транспортные расходы по доставке
продукции на расстояние lj от
поставщика в i-й
период времени в j-й
пункт потребления, р./км;
![]() - количество ездок (рейсов), совершаемое
автомобилем в i-й
период времени в j-й
пункт потребления;
- количество ездок (рейсов), совершаемое
автомобилем в i-й
период времени в j-й
пункт потребления;
![]() - штраф за задержку поставки 1 лотка в i-й период времени в j-й пункт потребления, р./лот.;
- штраф за задержку поставки 1 лотка в i-й период времени в j-й пункт потребления, р./лот.;
![]() - спрос на готовую продукцию в i-й период времени в j-м пункте, лот.;
- спрос на готовую продукцию в i-й период времени в j-м пункте, лот.;
![]() - организационные сборы на доставку
продукции (уведомление о прибытии, оформление документов, канцелярские расходы
и т.д.) в i-й период времени в j-й пункт потребления, р.;
- организационные сборы на доставку
продукции (уведомление о прибытии, оформление документов, канцелярские расходы
и т.д.) в i-й период времени в j-й пункт потребления, р.;
yн - ночной запас готовой продукции, предназначенный для первоочередного вывоза в 1 период времени, лот.;
![]() - штраф за задержку вывоза ночного запаса
продукции yсв от
поставщика в i-й
период времени в j-й
пункт, р./лот.;
- штраф за задержку вывоза ночного запаса
продукции yсв от
поставщика в i-й
период времени в j-й
пункт, р./лот.;
rj - спрос на готовую продукцию в j-м пункте потребления, лот.;
x1,x2 - производственная программа выпуска готовой продукции в 1 и 2 период времени соответственно, лот.
Организационные сборы ![]() равны нулю, если xij =0 , и
равны постоянной
равны нулю, если xij =0 , и
равны постоянной ![]() , если xij >0 .
Штраф
, если xij >0 .
Штраф ![]() способствует завозу продукции потребителям
в соответствии со спросом, т.е. обеспечивается максимальное реагирование на
изменяющийся спрос. Штраф
способствует завозу продукции потребителям
в соответствии со спросом, т.е. обеспечивается максимальное реагирование на
изменяющийся спрос. Штраф ![]() регламентирует вывоз
ночного запаса продукции от поставщика, равномерно распределенного по N потребителям.
регламентирует вывоз
ночного запаса продукции от поставщика, равномерно распределенного по N потребителям.
Обозначим
через ![]() общие потери (затраты и штрафы),
связанные с доставкой готовой продукции в размере x1j и отправляемой от поставщика
в первый период времени в j-й пункт потребления, а через g2(rj-x1j) - общие потери,
связанные с доставкой готовой продукции в размере x2j =rj- x1j и отправляемой от
поставщика во 2-й период времени в j-й пункт потребления.
общие потери (затраты и штрафы),
связанные с доставкой готовой продукции в размере x1j и отправляемой от поставщика
в первый период времени в j-й пункт потребления, а через g2(rj-x1j) - общие потери,
связанные с доставкой готовой продукции в размере x2j =rj- x1j и отправляемой от
поставщика во 2-й период времени в j-й пункт потребления.
Тогда
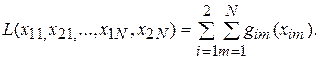 (4)
(4)
Обозначим через fj(x1) суммарные затраты при использовании оптимальной политики обслуживания j потребителей. Тогда оптимальное решение можно получить с помощью рекуррентных соотношений
![]() (5)
(5)
где x1j удовлетворяет условиям
![]() ; (6)
; (6)
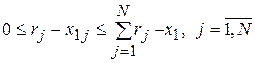 . (7)
. (7)
Областью
изменения переменной ![]() в (5) служит
в (5) служит 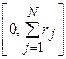 . Решая (5) с учетом ограничений (6)-(7),
получим оптимальное количество продукции, которое нужно доставить в i-й период времени в j-й пункт потребления.
. Решая (5) с учетом ограничений (6)-(7),
получим оптимальное количество продукции, которое нужно доставить в i-й период времени в j-й пункт потребления.
Решение задачи
Рассмотрим пример практической реализации модели на основе доставки хлебобулочных изделий 112 потребителям, дисперсно-расположенным на территории г. Кемерово. Процесс транспортного обслуживания потребителей в течение дня разбивается на утренний, дневной и вечерний завозы хлебобулочных изделий.
Спрос на готовую продукцию по периодам времени в каждом пункте потребления устанавливается в результате анкетного опроса или анализа соответствующих данных. При отсутствия такой информации может быть принято равномерное распределение спроса по периодам времени. Примерное распределение спроса в вечерний период представлено на рисунке 1, а суточный спрос на готовую продукцию по потребителям – на рисунке 2.
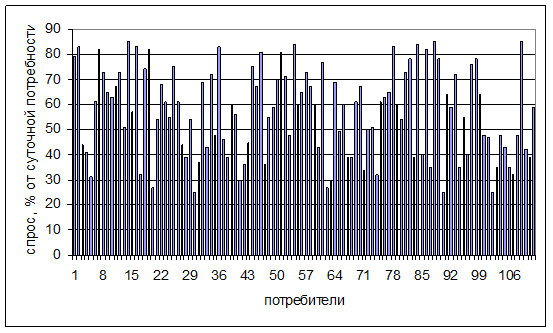
Рисунок 1. Доля вечернего спроса от суточной потребности, %
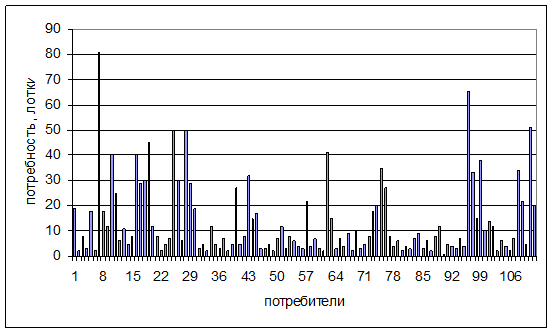
Рисунок 2. Суточный спрос готовой продукции по потребителям
Примем следующие значения экономических и технологических
параметров: ![]() = 20 р./км;
= 20 р./км; ![]() =120 р./лот.;
=120 р./лот.; ![]() = 10%
от
= 10%
от ![]() ;
; ![]() = 85
р./лот.;
= 85
р./лот.; ![]() = 600 лот.;
= 600 лот.; ![]() = 200
лот.
= 200
лот.
В результате решения задачи первого этапа получаем оптимальное распределение завоза продукции потребителям по периодам времени, фрагмент которого отражен в таблице.
Из таблицы видно, что преобладающая доля продукции доставляется потребителям утренним завозом, однако для некоторых получателей решающим становится дневной завоз (потребители 30,40,43-45, 111).
Таблица
Оптимальное распределение готовой продукции по периодам времени
|
№ потребителя
|
1 завоз
(утренний), лот. |
2 завоз
(дневной), лот. |
3 завоз
(вечерний), лот. |
Суточная
потребность, лот. |
|
1
|
13
|
4
|
2
|
19
|
|
3
|
4
|
2
|
2
|
8
|
|
4
|
2
|
1
|
0
|
3
|
|
5
|
11
|
5
|
2
|
18
|
|
7
|
66
|
13
|
2
|
81
|
|
8
|
15
|
2
|
1
|
18
|
|
16
|
35
|
3
|
2
|
40
|
|
17
|
26
|
2
|
1
|
29
|
|
29
|
11
|
16
|
2
|
29
|
|
30
|
4
|
13
|
2
|
19
|
|
33
|
0
|
2
|
0
|
2
|
|
40
|
9
|
16
|
2
|
27
|
|
43
|
9
|
21
|
2
|
32
|
|
44
|
1
|
12
|
2
|
15
|
|
45
|
4
|
11
|
2
|
17
|
|
46
|
1
|
2
|
0
|
3
|
|
47
|
0
|
2
|
1
|
3
|
|
111
|
8
|
41
|
2
|
51
|
|
112
|
4
|
10
|
6
|
20
|
Используя информацию из таблицы, на втором этапе формируем маршруты доставки с помощью известных методов [4-7].
Выводы
Гибко варьируя экономическими параметрами, можно определить устойчивость оптимального распределения, при котором темп выпуска и доставки хлебобулочных изделий получателям по периодам времени не изменится. Также можно установить доверительную вероятность уровня сервисного обслуживания потребителей, при котором не изменится уровень спроса в соответствующей торговой точке.
Уточнение функции затрат и параметров, влияющих на оптимальное решение, позволит правильно планировать выпуск хлебобулочных изделий, определять графики доставки продукции потребителям в приемлемый срок, планировать задействование автотранспорта на маршрутах, определять трудозатраты на этапе подготовки отгрузочных партий и в целом определять внепроизводственные расходы, влияющие на конечную цену готовой продукции.
Источники:
2. Тюрин А.Ю. Особенности формирования транспортных издержек и выбора подвижного состава в логистических системах пищевой промышленности// Вестник Кузбасского государственного технического университета. —2007. —No1. —С.121-123.
3. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования/Пер. с англ. под ред. А.А. Первозванского. —М.: Наука, 1965. —460 с.
4. Clark G., Write J. W.Scheduling of vehicles from central depot to a number delivery points// Operational Research Quarterly. —1964. —Vol. 12. —No 4. —Рp. 568-581.
5. Fisher M., Jaikumar R. A generalized assignment heuristic for vehicle routing// Networks. —1981. —Vol. 11. —No 1. —Pp. 109-124.
6. Koskosidis Y. A., Powell W.B. Clustering algorithms for consolidation of customer orders into vehicle shipments// Transportation Research. Part B. —1992. —Vol. 26B. —No 5. —Pp. 365-379.
7. Тюрин А.Ю. Эвристические методы решения задач доставки мелкопартионных грузов// Вестник Кузбасского государственного технического университета. —2007. —No 1. —С.51-55.
Страница обновлена: 26.03.2024 в 14:42:58
